Simple Proofs with Phantom Encoding
Phantom types. They’re a surprisingly potent tool for expressing how our systems should work.
Until recently, they’be eluded my understanding. In this post, I hope to elaborate on what they are and some simple ways they can be used to make programs safer and easier to maintain.
What Are Phantom Types?
Phantom types are bits of type information that aren’t exposed at the term level. That’s to say, their appearance in a data type declaration takes place only on the lefthand-side of the equal sign and does not not affect the runtime representation of datatypes. For example:
The polymorphic variable a does not influence how these types are stored or represented. What can we do with that? Here’s a sample of what I’ll explore in the rest of this post:
{-# LANGUAGE EmptyDataDecls #-}
-- enforce abstraction by limiting exported functions
module Data.Fun.With.Phantom (
bytes, unbytes,
encode, decode,
compress, decompress
) where
data Plain
data Encoded
data Decompressed
data Compressed
-- polymorphic phantom types `form` and `compressed`
newtype Bytes form compressed = Bytes ByteString
bytes :: ByteString -> Bytes Plain Decompressed
encode :: Bytes Plain Decompressed -> Bytes Encoded Decompressed
decode :: Bytes Encoded Decompressed -> Bytes Plain Decompressed
compress :: Bytes a Decompressed -> Bytes a Compressed
decompress :: Bytes a Compressed -> Bytes a Decompressed
unbytes :: Bytes a b -> ByteStringEnforcing Information Flow with Phantoms
The basic idea is: never lose track of what you’ve already done to a data type in your program. The example we’ll work through involves a ByteString that can be URL-encoded and/or compressed, and we want to ensure the following properties at compile-time with no runtime cost:
- A compressed ByteString should never be compressed again
- A decompressed ByteString should not be decompressed again
- A URL-encoded ByteString should not be encoded again
- An unencoded ByteString should not be decoded
- A plain ByteString may be URL-encoded
- A plain ByteString may be compressed
- A URL-encoded ByteString may be compressed
- A compressed ByteString can be decompressed, preserving the encoding data
It’s a little easier to see the properties we’re trying to enforce if we present this visually, like so:
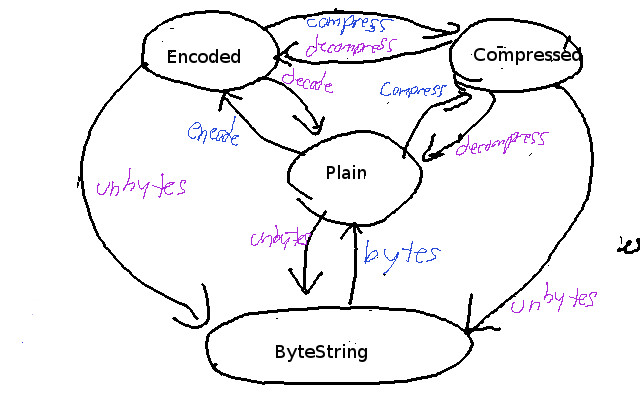
I hope that’s legible enough, in any case. This does bring up another interesting point: if you’re at the point where you can communicate your domain and all valid states in terms of diagrams like this, phantom types are an implementation detail. Diagrams and arrow-chasing become useful tools for communicating with others, whether they’re developers or not.
Onwards to more details!
A Closer Look at Implementation
Let’s take a closer look at the snippet I gave above:
The EmptyDataDecls language extension is what allows us to define datatypes that cannot be constructed, like data Plain and data Encoded. These serve as the set of type tags we use in defining our information flows.
-- polymorphic phantom types `form` and `compressed`
newtype Bytes form compressed = Bytes ByteStringHere, we lift our underlying datatype, ByteString, into our phantom-enhanced datatype Bytes. form is a polymorphic type variable that we’ll restrict to the tags Plain and Encoded. compressed is a polymorphic datatype that we’ll restrict to our tags Compressed and Uncompressed.
bytes :: ByteString -> Bytes Plain Decompressed
encode :: Bytes Plain Decompressed -> Bytes Encoded Decompressed
decode :: Bytes Encoded Decompressed -> Bytes Plain Decompressed
compress :: Bytes a Decompressed -> Bytes a Compressed
decompress :: Bytes a Compressed -> Bytes a Decompressed
unbytes :: Bytes a b -> ByteStringThese signatures capture all the valid transitions in our system. bytes and unbytes are the entry and exit points. encode and decode express the allowed transitions for URL-encoding operations. compress and decompress preserve the form information while updating the compression state at the type level.
What does the implementation of these signatures look like?
-- implemented for us via hackage libraries
GZ.compress :: ByteString -> ByteString
GZ.decompress :: ByteString -> ByteString
HTTP.urlEncode :: ByteString -> ByteString
HTTP.urlDecode :: ByteString -> ByteString
-- our interface
bytes = Bytes
unbytes (Bytes bs) = bs
compress (Bytes bs) = Bytes (GZ.compress bs)
decompress (Bytes bs) = Bytes (GZ.decompress bs)
encode (Bytes bs) = Bytes (HTTP.urlEncode bs)
decode (Bytes bs) = Bytes (HTTP.urlDecode bs)We just leverage existing libraries to do the work. With phantoms, all we’re doing is expressing the valid states and transitions for our particular system. That’s the beauty of it: it’s perfect for expressing what the core logic of a specialized system is.
Playing With Our Library
Let’s have a REPL session:
> :set -XOverloadedStrings
> let test = bytes "cat"
> :t test
test :: Bytes Plain Decompressed
> decode test
<interactive>:6:8:
Couldn't match type ‘Plain’ with ‘Encoded’
Expected type: Bytes Encoded Decompressed
Actual type: Bytes Plain Decompressed
> decompress test
Couldn't match type ‘Decompressed’ with ‘Compressed’
Expected type: Bytes Plain Compressed
Actual type: Bytes Plain Decompressed
> compress . compress . encode $ test
Couldn't match type ‘Compressed’ with ‘Decompressed’
Expected type: Bytes Encoded Decompressed
-> Bytes Encoded Decompressed
Actual type: Bytes Encoded Decompressed
-> Bytes Encoded Compressed
> -- preserves encoding information on decompress
> :t decompress . compress . encode $ test
test :: Bytes Encoded Decompressed
> :t decompress . compress $ test
test :: Bytes Plain Decompressed
> unbytes test
"cat"
> unbytes . compress $ test
"\US\139\b\NUL\NUL\NUL\NUL\NUL\NUL\ETXKN,\SOH\NUL\168C^\158\ETX\NUL\NUL\NUL"Great!
Preserving Abstraction with Phantoms
As we saw above, only valid transitions were allowed within the system. This is great! However, how do we take what we wrote and make it a safe kernel for others to use? We can use the familiar idea of information hiding to our benefit here. If users are unable to get at the underlying ByteString except through unbytes,
-- enforce abstraction by limiting exported functions
module Data.Fun.With.Phantom (
bytes, unbytes,
encode, decode,
compress, decompress
) whereThe system is opt-in. A user of this scheme wouldn’t have access to the newtype constructor, so they’re not allowed to escape the phantom net without using unbytes. As long as the operations are all expressed in terms of the exported functions, the safety properties hold.
Phantoms and Laws
Given that we’ve expressed our valid transitions carefully, there are still some run-time details we’d like to hold. Primarily, we’d like to think that inverse pairs of operations, when applied back-to-back, preserve the original input. These will be the laws that keep our system functional over refactorings and as we grow it. Let’s start by stating some laws we expect to hold true:
bytes . unbytes == id
unbytes . bytes == id
encode . decode == id
decode . encode == id
compress . decompress == id
decompress . compress == idAlright, let’s make this a QuickCheck spec:
{-# LANGUAGE GeneralizedNewtypeDeriving #-}
import Test.QuickCheck
instance Arbitrary ByteString where
arbitrary = fmap pack arbitrary
{-
Arbitrary, Eq, and Show needed for QuickCheck
if we change the expression of our laws so they always begin with a
ByteString and end with a ByteString, e.g., (unbytes . _ . bytes $
bs), then none of these instances are needed because we just proxy
to the underlying ByteString type.
-}
newtype Bytes form compressed = Bytes ByteString deriving (Arbitrary, Eq, Show)
prop_bytesUnbytesIdemp bs = (bytes . unbytes $ bs) == bs
prop_unbytesBytesIdemp bs = (unbytes . bytes $ bs) == bs
prop_encodeDecodeIdemp bs = (encode . decode $ bs) == bs
prop_decodeEncodeIdemp bs = (decode . encode $ bs) == bs
prop_compressDecompressIdemp bs = (compress . decompress $ bs) == bs
prop_decompressCompressIdemp bs = (decompress . compress $ bs) == bsLet’s run some tests!
> quickCheck prop_bytesUnbytesIdemp
+++ OK, passed 100 tests.
> quickCheck prop_unbytesBytesIdemp
+++ OK, passed 100 tests.
> quickCheck prop_compressDecompressIdemp
*** Failed! Exception: 'Codec.Compression.Zlib:
premature end of compressed stream' (after 1 test): Bytes ""Oh no! What happened? It turns out that GZip has a very particular header. We can fix this test by leveraging property combinators in QuickCheck to ensure that all strings that go through decompression first are generated in such a way that they have the correct header. We won’t cover this here.
Comparing Phantoms to Alternatives: Sums and Newtypes
Sum types are another means to express all valid elements in a domain. We can enumerate them below as follows:
data IsCompressed = YesCompress | NoCompress
data IsEncoded = YesEncoded | NoEncoded
newtype Bytes = Bytes ByteString IsEncoded IsCompressedOur restricted operations would then look like:
compress :: Bytes -> Maybe Bytes
compress (Bytes bs _ YesCompressed) = Nothing
compress (Bytes bs _ NoCompressed) = Just $It gets to be pretty verbose and pushes more error checking into the runtime space, and we do pay a run-time cost for using data constructors rather than newtypes.
An approach that uses newtypes entirely doesn’t fare much better:
newtype PlainDecompressedBytes = PlainDecompressedBytes ByteString
newtype EncodedDecompressedBytes = EncodedBytes ByteString
...Essentially, it amounts to defining a newtype for each transition path in the original graph. It gets clunky. It’s type-safe, but it won’t scale as more information of interest is added to the subsystem graph.
There are other options. Those options, however, begin with phantom types and add a bit more, say, GADTs + phantom types. These are beyond the scope of this post and beyond the realm of my current knowledge comfort zone.
Applying Phantom Types
Phantom types have seen use in many domains. I’ve just given a fairly basic example here. You’ll often see phantom types used in combination with other type system features, like GADTs. To share a few more applications I’ve seen:
- Optimizing FRP with GADTS: paper
- Session Types in Haskell: paper
- A Type Safe Term Language: GHC guide
- Ensuring Correct Encodings: blog
More resources are attached at the end of this post.
Caveats
The primary limitation of phantom types is that you must think carefully about your domain. Can you specify all the transitions? If you find yourself reaching for the underlying data type often, it may be a sign that you need to extend your safe kernel. Phantoms allows some of this easily, since they’re (usually) polymorphic over their domain. For example, adding a Functor instance for our Bytes type can be as simple as:
{-# LANGUAGE DerivingFunctor #-}
newtype Bytes form compressed = Bytes ByteString deriving (Functor)Add what you need as you need it. The phantom type approach to development is very friendly to iterative enhancement.
Phantom Types in Your Language
I have a firm inclination towards Haskell. However, know that compile-time phantom type techniques are not unique. In particular, I expect that all the following languages support this in some shape or form:
- Scala
- Rust
- OCaml
- Standard ML
- Swift
- Purescript
- Elm
- Agda
- Coq
- Idris
As far as my understanding of phantom types goes, it seems that in order for a language to support these techniques, it needs to have:
- Parametric polymorphism
- A means to create type tags
What’s Next?
Fiddle with phantoms.
Read up on a domain that is closer to your own. As far as I can tell, people have been doing creative things with phantom types as early as the 1990s. A lot has been written on the subject.
Go have fun! (because Phantom types are spooky cool)
Additional Resources
- Code
- Fun with Phantom Types (paper) (slides) (Mar. 2003)
- Fun with Type Functions (paper) (May 2010)
- Practical Datatype Specialization with Phantom Types and Recursion Schemes (paper) (2005)
- Phantom Types and Subtyping (paper) (2006)
- What are good applications of Phantom types? (quora) (May 2011)
- Phantom Types (Haskell wiki (Mar. 2013)
- Phantom Types: Haskell Wikibook (wiki) (Jan. 2013)
- Phantom Types (Swift) (blog)
- Using Phantom Types for Extra Safety (blog) (Jul. 2014)
- Phantom Types in Rust (blog) (Aug. 2013)
- Phantom Types in Haskell and Scala (blog) (Oct. 2010)
- What is an Indexed Monad? (Stack Overflow) (Feb. 2015)
- What I Wish I Knew When Learning Haskell (article) (2015)